The universal behavior of a disordered system

The Landau theory of phase transitions and the concept of symmetry breaking provide a unifying description of even such seemingly different many-body systems as a paramagnet cooled to the verge of ferromagnetic order or a metal approaching the superconducting transition. What happens, however, when these systems can lose energy to their environment? For example, in rare-earth compounds called “heavy-fermion” materials, the f-shell magnetic moments interact with a sea of mobile electrons [1]. Similarly, near the metal-superconductor transition in ultrathin wires, the electrons pair up in a connected network of small, superconducting puddles that are surrounded by a bath of unpaired metallic electrons [2]. The surrounding metal gives rise to a parallel resistive channel and hence dissipation. Introducing dissipation into a many-body quantum mechanical problem presented a theoretical challenge that was only resolved in the last quarter of the 20th century [3, 4, 5].

Phase transitions in quantum systems with both dissipation and disorder are, not surprisingly, even more complicated. Whether we like it or not, all experimental systems, and especially the examples above, have some degree of disorder such as a structural imperfection or the presence of impurities. Therefore understanding the effects of disorder is not merely an abstract intellectual challenge, it is necessary for explaining what we actually measure in these systems. In particular, even a small amount of disorder can have a big effect in low-dimensional quantum systems, where ordering is more difficult and interaction effects are enhanced. A notable example is Philip Anderson’s discovery of localization in metals (see his Nobel address [6]).

In a paper appearing in Physical Review B, Thomas Vojta and Chetan Kotabage of the Missouri University of Science and Technology and José Hoyos, now at Duke University, provide yet another example of the profound impact that disorder has on a large class of low-dimensional quantum systems [7]. In their paper, they derive the theory for a quantum phase transition in a one-dimensional system that is akin to both the magnetic and superconducting examples noted above: a chain of magnetic moments, whose motion is dissipative, and whose local interaction parameters are random. Unlike previous work, Vojta, Kotabage, and Hoyos tackle both dissipation and randomness on equal footing. Despite the complexity of this problem, they find the low-energy behavior of such dissipative random chains through a series of intuitive and simple arguments. Furthermore, they demonstrate that the low-energy behavior is independent of the type and amount of disorder in the chain. That is, it is universal.

To understand this perhaps unintuitive result, we first discuss the concept of universality and explain how it arises in random systems using a simple example. The term universality entered our vocabulary with the development of renormalization group theory, which was based on the realization that an important but overlooked symmetry of nature is scale invariance [8]. This symmetry is not omnipresent. Rather, it describes systems at critical points on the boundary between two phases, for instance, between a ferromagnet and a paramagnet. As a paramagnet is cooled to the verge of ferromagnetism, finite, strongly magnetized droplets start to form, albeit with each droplet pointing in a different direction. At the critical point, these droplets appear in all sizes, and if we zoom out, the size distribution of the droplets looks the same. But, if zooming out leaves the system looking the same, this is equivalent to saying that microscopic details are unimportant in determining the magnet’s behavior. This insensitivity to microscopic details is called universality. (We should add that in a quantum system, zooming out is tantamount to only looking at fluctuations on large length scales, or, equivalently, at the low-energy behavior.)

Typically, the description of a nondisordered, many-body quantum system begins with translational invariance and momentum conservation. Such a system of particles can be described by a set of states with a well-defined momentum denoted by the wave number k. A useful example of a simple many-body problem that we can solve in this way is the one-dimensional “tight-binding” model of noninteracting fermions, in which each fermion is tightly bound to a site on a chain, but can hop to a neighboring site with probability t. The energy spectrum for this model has a simple form: εk=-2t cos(k).

What happens, however, when translational invariance is broken? For our purposes, we can still use the hopping-fermion model, but let the hopping strength t depend on where the fermion is on the chain: t⇒ti. Instinctively, we would anticipate that the appearance of nonuniformity in this fermion-hopping system would mangle the neat cosine form of the energy spectrum and replace it with a random and noisy spectrum that crucially depends on the details of how the hopping varies from site to site. Quite surprisingly, however, the opposite seems to occur: the disorder introduced through the randomness in the hopping gives rise to an energy spectrum of the fermion states that, albeit different from the pure system’s cosine spectrum, is essentially independent of the details of the disorder. This is also the essence of universality in disordered quantum systems: the low-energy physical properties are independent of the disorder distribution.

The system that Vojta, Kotabage, and Hoyos analyze has much in common with the simple fermion-hopping problem, and it can be solved by the same method: real-space renormalization group. Shang-keng Ma, Chandan Dasgupta, and Chin-kun Hu of the University of California, San Diego proposed this method in 1979 to solve the problem of random interactions between spins on a chain [9]. We can demonstrate and use their basic arguments to understand the random-hopping problem described above.

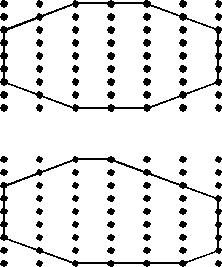
We begin by concentrating on the strongest hopping element, tmax, and ignore everything else in the Hamiltonian as a much weaker perturbation. A fermion put in two neighboring sites, say 1 and 2, with tmax hopping between them, can minimize its energy by choosing to be in the symmetric superposition |ϕ〉=|1〉+|2〉, which has the energy ε-=-tmax. In fact, this fermion gets stuck in this bond between the two sites, since anywhere else it would have a higher energy. But fermions from neighboring sites, say site 0, can also hop to site 1, locking the first fermion inserted in the bond between the two sites at site 2. This is an excited state with energy ε=0. This predicament can resolve itself with the fermion of site 2 hopping to site 3, leaving one fermion behind in the state |ϕ〉=|1〉+|2〉 with energy of ε=-tmax. This looks as if a fermion hopped directly from site 0 to site 3, leaving the two sites 1 and 2 untouched. So, we might as well forget sites 1 and 2 and solve a new Hamiltonian in which a small “renormalized” t0,3 connects sites 0 and 3. Repeating this procedure with the strongest bond at each stage will result in all fermions inserted localized between two sites, which can be arbitrarily far apart (Fig. 1). From this procedure, we can extract the energy of the fermions’ states: a fermion localized between two sites L links apart will have a binding energy E obeying ln E~-(L)1/2 [10].

Vojta, Kotabage, and Hoyos have shown that a similar real-space analysis applies quite generally to dissipative disordered chains on the verge of a symmetry-breaking phase transition. Their focus is on a system that is similar to a chain of dynamically fluctuating magnetons (magnetic moments that can be described by a single variable). Each magneton interacts ferromagnetically with its nearest neighbors and has an energy scale ri associated with its dynamic fluctuations. These fluctuations compete with the energy scale Ji that prefers neighboring magnetons to align with one another and seeks to establish magnetic order. Just as we solved the hopping-fermion problem above, Vojta, Kotabage, and Hoyos show that we can solve the disordered dissipative quantum magnet by either (a) iteratively eliminating the most fluctuating magneton (the moment with the largest ri), which results in a ferromagnetic interaction between its neighbors, or (b) allowing the two most strongly interacting neighbors (i.e., those with the strongest Ji between them), to unite and form a single magneton, with a renormalized lower energy scale, r, of the dynamic fluctuations. A sketch of the resulting state is shown in the bottom of Fig. 2. This, they show, results in essentially the same universal behavior as is found in fermions in the random-hopping chain. Physically, this problem describes the critical behavior of superconducting puddles that form in a metallic wire right above the superconducting transition temperature (top of Fig. 2 ).

Vojta, Kotabage, and Hoyos go beyond solving the model to show that dissipative one-dimensional systems close to criticality are always susceptible to disorder. The ground-state properties of such systems cannot be analyzed using perturbation theory near the point of translational invariance. The results force us to reevaluate much of the research done on superconducting wires and magnetic chains, and to pose the question: How many other low-dimensional electronic systems can be described in the same way and have the same low-energy properties? What properties, so far taken for granted, are altered due to the presence of even a small amount of disorder? As the work of Vojta, Kotabage, and Hoyos proves, the combination of disorder, interactions, and low dimensionality (which enhances fluctuations) is bound to provide us with more surprises and fascinating examples of disorder-dominated phases, waiting to be discovered.

Illustration: Alan Stonebraker

Separate Window | Enlarge

Figure 1: Fermions on the random-hopping chain. Instead of moving freely throughout the chain, fermions are confined to pairs of sites (connected by the arcs), which are often nearest neighbors, but can also be very far apart. The pair formation is scale invariant: if we zoom out, and only draw sites that are separated by a distance matching our new reduced resolution, the localization pattern looks the same.

Illustration: Alan Stonebraker

Separate Window | Enlarge

Figure 2: (top) The model from Vojta, Kotabage, and Hoyos can describe what happens when an ultrathin metallic wire is cooled to the verge of turning into a superconductor. Superconducting puddles (orange) are connected to their neighbors through “weak links“ in a metallic environment. Because the superconductivity in each puddle is described by a complex order parameter, the puddles can be modeled as planar magnetons, with a magnitude and direction that correspond to the amplitude and phase of the order parameter, respectively. The metallic environment induces dissipation and dampens fluctuations of the order parameter. (bottom) Restricting ourselves to the language of magnetons, we sketch out how the details on small length scales become unimportant to the description of the system. Grain 4 fluctuates so much that its effective magnetic moment is destroyed. Next, grains 2 and 3 unite because of the strong magnetic coupling between them, and point in the same direction, but they too can diminish due to strong resulting fluctuations. Finally, grains 1 and 5 unite due to a resulting coupling between them.

http://physics.aps.org/articles/v2/1

Edymar Gonzalez A

C.I:19.502.773

CRF

Quantum Entanglement Achieved in Solid-State Circuitry

ScienceDaily (Jan. 12, 2010) — For the first time, physicists have convincingly demonstrated that physically separated particles in solid-state devices can be quantum-mechanically entangled. The achievement is analogous to the quantum entanglement of light, except that it involves particles in circuitry instead of photons in optical systems.

Both optical and solid-state entanglement offer potential routes to quantum computing and secure communications, but solid-state versions may ultimately be easier to incorporate into electronic devices.

In optical entanglement experiments, a pair of entangled photons may be separated via a beam splitter. Despite their physical separation, the entangled photons continue to act as a single quantum object. A team of physicists from France, Germany and Spain has now performed a solid-state entanglement experiment that uses electrons in a superconductor in place of photons in an optical system.

As conventional superconducting materials are cooled, the electrons they conduct entangle to form what are known as Cooper pairs. In the new experiment, Cooper pairs flow through a superconducting bridge until they reach a carbon nanotube that acts as the electronic equivalent of a beam splitter. Occasionally, the electrons part ways and are directed to separate quantum dots -- but remain entangled. Although the quantum dots are only a micron or so apart, the distance is large enough to demonstrate entanglement comparable to that seen in optical systems.

In addition to the possibility of using entangled electrons in solid-state devices for computing and secure communications, the breakthrough opens a whole new vista on the study of quantum mechanically entangled systems in solid materials.

The experiment is reported in an upcoming issue of Physical Review Letters and highlighted with a Viewpoint in the January 11 issue of Physics.

This is an SEM image of a typical Cooper pair splitter. The bar is 1 micrometer. A central superconducting electrode (blue) is connected to two quantum dots engineered in the same single wall carbon nanotube (in purple). Entangled electrons inside the superconductor can be coaxed to move in opposite directions in the nanotube, ending up at separate quantum dots, while remaining entangled. (Credit: L.G. Herrmann, F. Portier, P. Roche, A. Levy Yeyati, T. Kontos, and C. Strunk)

http://www.sciencedaily.com/releases/2010/01/100111091222.htm

Edymar Gonzalez A

C.I: 19.502.773

CRF

Why Certain Symmetries Are Never Observed in Nature

ScienceDaily (Mar. 31, 2010) — Nature likes some symmetries, but dislikes others. Ordered solids often display a so-called 6-fold rotation symmetry. To achieve this kind of symmetry, the atoms in a plane surround themselves with six neighbours in an arrangement similar to that found in honeycombs. As opposed to this, ordered materials with 7-fold, 9-fold or 11-fold symmetries are never observed in nature.

Researchers from the Max Planck Institute for Metals Research, the University of Stuttgart and the TU Berlin discovered the reason for this when they tried to impose a 7-fold symmetry on a layer of charged colloidal particles using strong laser fields: the emergence of ordered structures requires the presence of specific sites where the corresponding order nucleates. Indeed, such nuclei are present in large numbers in exactly those structures for which nature shows a preference. In contrast, they only arise sporadically in patterns with 7-fold symmetry.

The process involved here sounds unwieldy, but is, in fact, quite simple: a material has a 6-fold rotation symmetry if the arrangement of its atoms remains unchanged when it is rotated by 60 degrees -- one sixth of a circle. The atoms in metals often order themselves in this way. However, more complicated structures with 5-fold, 8-fold or 10-fold rotation symmetry also exist. "It is surprising that materials with 7-fold, 9-fold or 11-fold symmetry have not yet been observed in nature," says Clemens Bechinger, fellow at the Max Planck Institute for Metals Research and Professor at the University of Stuttgart: "This is all the more astonishing in view of the fact that patterns with any rotation symmetry can be drawn without difficulty on paper." The question is, therefore, whether such materials have simply been overlooked up to now or whether nature has an aversion to certain symmetries.

This is the question that Clemens Bechinger has been investigating with his colleagues. "The answer is of interest to us both from a fundamental point of view but also because it could be helpful for tailoring materials with novel properties for technical applications," explains the physicist. The characteristics of a material are generally very dependent on its rotation symmetry. Graphite and diamond, for example, both consist of carbon atoms and differ solely in their crystal symmetry.

To produce materials with 7-fold symmetry, which do not actually exist in nature, the researchers resorted to a special trick: they superimposed seven laser beams and thereby generated a light pattern with 7-fold symmetry. They then introduced a layer of colloidal particles approximately three micrometers in diameter into the laser field. The effect of the electromagnetic field of the light pattern on the particles is akin to the formation of a mountain landscape, in which they tend to gravitate to the valleys. The colloidal particles, which repel each other because of their electric charges, attempt, in turn, to form a 6-fold symmetrical structure.

The researchers raise the profile of the light landscape by gradually increasing the intensity of the lasers. In this way, they exert increasing pressure on the colloidal particles to form a 7-fold symmetry instead of a 6-fold one. "This enables us to ascertain the laser intensity up to which the particles do not adept the 7-fold order and retain their 6-fold symmetry," says Jules Mikhael, the doctoral student working on the project.

In the same way, the physicists subjected the particles to a 5-fold light lattice and observed a clear difference: the particles clearly avoid a 7-fold symmetry and assume the 5-fold symmetry at relatively low laser intensities. Therefore, nature's rejection of 7-fold symmetries is also demonstrated in the model system created by the researchers in Stuttgart.

"What is crucial, however, is that our experiment also uncovers the reason why the particles stubbornly refuse to form a 7-fold structure," notes Clemens Bechinger. When the physicists increase the laser intensity, the particles initially only assume a 7-fold symmetry in very isolated places. Only when the intensity is further increased does the order spread to the entire sample. The researchers identified certain structures in the light pattern as the starting point for the 7-fold symmetry. These consist of a central point of light, which is surrounded by a ring of other light points and is, therefore, strongly reminiscent of a flower blossom.

"In the light pattern with 5-fold symmetry we find around 100 times more of these flower-shaped centres than in that with the 7-fold pattern," explains Michael Schmiedeberg. The density of these nuclei clearly plays the crucial role. The higher the density, the less force the researchers must exert to generate structures of the corresponding rotation symmetry. In this case, low light intensity is sufficient for the relevant order to spread from the centre.

The differences in the densities of the flower-shaped nuclei alone also explains why 8-fold and 10-fold symmetries arise in nature but 9-fold and 11-fold ones do not. "The result is astonishing because it involves a simple geometric argument," says Bechinger: "It is completely independent on the special nature of the interaction between the particles, and applies, therefore, both to our colloidal systems and to atomic systems."

The experiments explain, first, why it is no coincidence that materials with certain symmetries are not found in nature. Second, they demonstrate a concrete way, in which such structures can be made artificially in colloidal systems -- that is with the help of external fields. This could be useful for the production of photonic crystals with unusual symmetries in which, for example, individual layers of colloids with 7-fold rotation symmetry are stacked on top of each other. Photonic crystals consist of microstructures, which affect light waves in a similar way to that in which crystal lattices affect electrons. Due to the higher rotation symmetry, the optical characteristics of 7-fold photonic crystals would be less dependent on the angle of incidence of a beam of light than the existing photonic crystals with 6-fold symmetry.

In addition to this, materials with unconventional symmetries have other interesting characteristics, for example very low frictional resistance. As a result they can reduce the friction between sliding parts e.g. in engines when applied as thin surface coatings. "Overall the search for materials with unusual rotation symmetries is of considerable interest," says Clemens Bechinger: "Our results can help to identify the particular symmetries that are worth looking for."

Symmetry bears flowers: The Stuttgart-based researchers generate light patterns by superimposing several laser beams. Flower-shaped structures form in the laser patterns which act as a nucleus for order. They arise very rarely in the 7-fold pattern (bottom left) - therefore no materials with a 7-fold symmetry are found in nature. (Credit: Jules Mikhael, University of Stuttgart)


http://www.sciencedaily.com/releases/2010/03/100330102747.htm

Edymar Gonzalez A

19.502.773

CRF

Examine the Elementary Excitations

Its amazing how slow human beings are. The atoms inside your eyelash collide with one another a million million times during each time you blink your eye. It's not surprising, then, that we spend most of our time in condensed--matter physics studying those things in materials that happen slowly. Typically only vast conspiracies of immense numbers of atoms can produce the slow behavior that humans can perceive.

Figure 8. One dimensional crystal: phonons.
The order parameter field for a one--dimensional crystal is the local displacement u(x). Long-wavelength waves in u(x) have low frequencies, and cause sound.
Crystals are rigid because of the broken translational symmetry. Because they are rigid, they fight displacements. Because there is an underlying translational symmetry, a uniform displacement costs no energy. A nearly uniform displacement, thus, will cost little energy, and thus will have a low frequency. These low-frequency elementary excitations are the sound waves in crystals.

A good example is given by sound waves. We won't talk about sound waves in air: air doesn't have any broken symmetries, so it doesn't belong in this lecture. Consider instead sound in the one-dimensional crystal shown in figure 8. We describe the material with an order parameter field u(x), where here x is the position within the material and x - u(x) is the position of the reference atom within the ideal crystal.

Now, there must be an energy cost for deforming the ideal crystal. There won't be any cost, though, for a uniform translation: u(x)u0 has the same energy as the ideal crystal. (Shoving all the atoms to the right doesn't cost any energy.) So, the energy will depend only on derivatives of the function u(x). The simplest energy that one can write looks like

(2)

(Higher derivatives won't be important for the low frequencies that humans can hear.) Now, you may remember Newton's law F=m a. The force here is given by the derivative of the energy F=-(d/du). The mass is represented by the density of the material . Working out the math (a variational derivative and an integration by parts, for those who are interested) gives us the equation

(3)

The solutions to this equation

(4)

represent phonons or sound waves. The wavelength of the sound waves is , and the frequency is . Plugging (4) into (3) gives us the relation

(5)

The frequency gets small only when the wavelength gets large. This is the vast conspiracy: only huge sloshings of many atoms can happen slowly. Why does the frequency get small? Well, there is no cost to a uniform translation, which is what (4) looks like for infinite wavelength. Why is there no energy cost for a uniform displacement? Well, there is a translational symmetry: moving all the atoms the same amount doesn't change their interactions. But haven't we broken that symmetry? That is precisely the point.

Long after phonons were understood, Jeffrey Goldstone started to think about broken symmetries and order parameters in the abstract. He found a rather general argument that, whenever a continuous symmetry (rotations, translations, SU(3), ...) is broken, long-wavelength modulations in the symmetry direction should have low frequencies. The fact that the lowest energy state has a broken symmetry means that the system is stiff: modulating the order parameter will cost an energy rather like that in equation equation (2). In crystals, the broken translational order introduces a rigidity to shear deformations, and low frequency phonons (figure 8). In magnets, the broken rotational symmetry leads to a magnetic stiffness and spin waves (figure 9a). In nematic liquid crystals, the broken rotational symmetry introduces an orientational elastic stiffness (it pours, but resists bending!) and rotational waves (figure 9b).

Figure 9A. Magnets: spin waves.
Magnets break the rotational invariance of space. Because they resist twisting the magnetization locally, but don't resist a uniform twist, they have low energy spin wave excitations.

Figure 9B. Nematic liquid crystals: rotational waves.
Nematic liquid crystals also have low-frequency rotational waves.

In superfluids, the broken gauge symmetry leads to a stiffness which results in the superfluidity. Superfluidity and superconductivity really aren't any more amazing than the rigidity of solids. Isn't it amazing that chairs are rigid? Push on a few atoms on one side, and atoms away atoms will move in lock-step. In the same way, decreasing the flow in a superfluid must involve a cooperative change in a macroscopic number of atoms, and thus never happens spontaneously any more than two parts of the chair ever drift apart.

The low-frequency Goldstone modes in superfluids are heat waves! (Don't be jealous: liquid helium has rather cold heat waves.) This is often called second sound, but is really a periodic modulation of the temperature which passes through the material like sound does through a metal.

O.K., now we're getting the idea. Just to round things out, what about superconductors? They've got a broken gauge symmetry, and have a stiffness to decays in the superconducting current. What is the low energy excitation? It doesn't have one. But what about Goldstone's theorem? Well, you know about physicists and theorems ...

That's actually quite unfair: Goldstone surely had conditions on his theorem which excluded superconductors. It's just that everybody forgot the extra conditions, and just remembered that you always got a low frequency mode when you broke a continuous symmetry. We of course understood all along why there isn't a Goldstone mode for superconductors: my advisor, Phillip W. Anderson, showed that it's related to the Meissner effect. The high energy physicists forgot, though, and had to rediscover it for themselves. Now we all call the loophole in Goldstone's theorem the Higgs mechanism, because (to be truthful) Higgs and his high-energy friends found a much simpler and more elegant explanation than we had. We'll discuss Meissner effects and the Higgs mechanism in the next lecture.

I'd like to end this section, though, by bringing up another exception to Goldstone's theorem: one we've known about even longer, but which we don't have a nice explanation for. What about the orientational order in crystals? Crystals break both the continuous translational order and the continuous orientational order. The phonons are the Goldstone modes for the translations, but there are no orientational Goldstone modes. We'll discuss this further in the next lecture, but I think this is one of the most interesting unsolved basic questions in the subject.

Examine the Elementary Excitations

ts amazing how slow human beings are. The atoms inside your eyelash collide with one another a million million times during each time you blink your eye. It's not surprising, then, that we spend most of our time in condensed--matter physics studying those things in materials that happen slowly. Typically only vast conspiracies of immense numbers of atoms can produce the slow behavior that humans can perceive.

Figure 8. One dimensional crystal: phonons.
The order parameter field for a one--dimensional crystal is the local displacement u(x). Long-wavelength waves in u(x) have low frequencies, and cause sound.
Crystals are rigid because of the broken translational symmetry. Because they are rigid, they fight displacements. Because there is an underlying translational symmetry, a uniform displacement costs no energy. A nearly uniform displacement, thus, will cost little energy, and thus will have a low frequency. These low-frequency elementary excitations are the sound waves in crystals.

A good example is given by sound waves. We won't talk about sound waves in air: air doesn't have any broken symmetries, so it doesn't belong in this lecture. Consider instead sound in the one-dimensional crystal shown in figure 8. We describe the material with an order parameter field u(x), where here x is the position within the material and x - u(x) is the position of the reference atom within the ideal crystal.

Now, there must be an energy cost for deforming the ideal crystal. There won't be any cost, though, for a uniform translation: u(x)u0 has the same energy as the ideal crystal. (Shoving all the atoms to the right doesn't cost any energy.) So, the energy will depend only on derivatives of the function u(x). The simplest energy that one can write looks like

(2)

(Higher derivatives won't be important for the low frequencies that humans can hear.) Now, you may remember Newton's law F=m a. The force here is given by the derivative of the energy F=-(d/du). The mass is represented by the density of the material . Working out the math (a variational derivative and an integration by parts, for those who are interested) gives us the equation

(3)

The solutions to this equation

(4)

represent phonons or sound waves. The wavelength of the sound waves is , and the frequency is . Plugging (4) into (3) gives us the relation

(5)

The frequency gets small only when the wavelength gets large. This is the vast conspiracy: only huge sloshings of many atoms can happen slowly. Why does the frequency get small? Well, there is no cost to a uniform translation, which is what (4) looks like for infinite wavelength. Why is there no energy cost for a uniform displacement? Well, there is a translational symmetry: moving all the atoms the same amount doesn't change their interactions. But haven't we broken that symmetry? That is precisely the point.

Long after phonons were understood, Jeffrey Goldstone started to think about broken symmetries and order parameters in the abstract. He found a rather general argument that, whenever a continuous symmetry (rotations, translations, SU(3), ...) is broken, long-wavelength modulations in the symmetry direction should have low frequencies. The fact that the lowest energy state has a broken symmetry means that the system is stiff: modulating the order parameter will cost an energy rather like that in equation equation (2). In crystals, the broken translational order introduces a rigidity to shear deformations, and low frequency phonons (figure 8). In magnets, the broken rotational symmetry leads to a magnetic stiffness and spin waves (figure 9a). In nematic liquid crystals, the broken rotational symmetry introduces an orientational elastic stiffness (it pours, but resists bending!) and rotational waves (figure 9b).

Figure 9A. Magnets: spin waves.
Magnets break the rotational invariance of space. Because they resist twisting the magnetization locally, but don't resist a uniform twist, they have low energy spin wave excitations.

Figure 9B. Nematic liquid crystals: rotational waves.
Nematic liquid crystals also have low-frequency rotational waves.

In superfluids, the broken gauge symmetry leads to a stiffness which results in the superfluidity. Superfluidity and superconductivity really aren't any more amazing than the rigidity of solids. Isn't it amazing that chairs are rigid? Push on a few atoms on one side, and atoms away atoms will move in lock-step. In the same way, decreasing the flow in a superfluid must involve a cooperative change in a macroscopic number of atoms, and thus never happens spontaneously any more than two parts of the chair ever drift apart.

The low-frequency Goldstone modes in superfluids are heat waves! (Don't be jealous: liquid helium has rather cold heat waves.) This is often called second sound, but is really a periodic modulation of the temperature which passes through the material like sound does through a metal.

O.K., now we're getting the idea. Just to round things out, what about superconductors? They've got a broken gauge symmetry, and have a stiffness to decays in the superconducting current. What is the low energy excitation? It doesn't have one. But what about Goldstone's theorem? Well, you know about physicists and theorems ...

That's actually quite unfair: Goldstone surely had conditions on his theorem which excluded superconductors. It's just that everybody forgot the extra conditions, and just remembered that you always got a low frequency mode when you broke a continuous symmetry. We of course understood all along why there isn't a Goldstone mode for superconductors: my advisor, Phillip W. Anderson, showed that it's related to the Meissner effect. The high energy physicists forgot, though, and had to rediscover it for themselves. Now we all call the loophole in Goldstone's theorem the Higgs mechanism, because (to be truthful) Higgs and his high-energy friends found a much simpler and more elegant explanation than we had. We'll discuss Meissner effects and the Higgs mechanism in the next lecture.

I'd like to end this section, though, by bringing up another exception to Goldstone's theorem: one we've known about even longer, but which we don't have a nice explanation for. What about the orientational order in crystals? Crystals break both the continuous translational order and the continuous orientational order. The phonons are the Goldstone modes for the translations, but there are no orientational Goldstone modes. We'll discuss this further in the next lecture, but I think this is one of the most interesting unsolved basic questions in the subject.

http://www.lassp.cornell.edu/sethna/OrderParameters/ElementaryExcitations.html

Edymar Gonzalez A

19.502.773

CRF

Identify the Broken Symmetry

What is it which distinguishes the hundreds of different states of matter? Why do we say that water and olive oil are in the same state (the liquid phase), while we say aluminum and (magnetized) iron are in different states? Through long experience, we've discovered that most phases differ in their symmetry.

Figure 2. Which is more symmetric?
The cube has many symmetries. It can be rotated by 90 degrees, 180 degrees, or 270 degrees about any of the three axes passing through the faces. It can be rotated by 120 degrees or 240 degrees about the corners, and by 180 degrees about an axis passing from the center through any of the 12 edges. The sphere, though, can be rotated by any angle. The sphere respects rotational invariance: all directions are equal. The cube is an object which breaks rotational symmetry: once the cube is there, some directions are more equal than others.

Consider figure 2, showing a cube and a sphere. Which is more symmetric? Clearly, the sphere has many more symmetries than the cube. One can rotate the cube by 90 degrees in various directions and not change its appearance, but one can rotate the sphere by any angle and keep it unchanged.

Figure 3. Which is more symmetric?
At first glance, water seems to have much less symmetry than ice. The picture of ``two--dimensional'' ice clearly breaks the rotational invariance: it can be rotated only by 120 degrees or 240 degrees It also breaks the translational invariance: the crystal can only be shifted by certain special distances (whole number of lattice units). The picture of water has no symmetry at all: the atoms are jumbled together with no long--range pattern at all. Water, though, isn't a snapshot: it would be better to think of it as a combination of all possible snapshots! Water has a complete rotational and translational symmetry: the pictures will look the same if the container is tipped or shoved.

In figure 3, we see a 2-D schematic representation of ice and water. Which state is more symmetric here? Naively, the ice looks much more symmetric: regular arrangements of atoms forming a lattice structure. The water looks irregular and disorganized. On the other hand, if one rotated figure 3B by an arbitrary angle, it would still look like water! Ice has broken rotational symmetry: one can rotate figure 3A only by multiples of 60 degrees. It also has a broken translational symmetry: it's easy to tell if the picture is shifted sideways, unless one shifts by a whole number of lattice units. While the snapshot of the water shown in the figure has no symmetries, water as a phase has complete rotational and translational symmetry.

One of the standard tricks to see if two materials differ by a symmetry is to try to change one into the other smoothly. Oil and water won't mix, but I think oil and alcohol do, and alcohol and water certainly do. By slowly adding more alcohol to oil, and then more water to the alcohol, one can smoothly interpolate between the two phases. If they had different symmetries, there must be a first point when mixing them when the symmetry changes, and it is usually easy to tell when that phase transition happens.

http://www.lassp.cornell.edu/sethna/OrderParameters/BrokenSymmetry.html

Edymar Gonzalez A

19.502.773

CRF

Crystal Morphology and Crystal Symmetry

The symmetry observed in crystals as exhibited by their crystal faces is due to the ordered internal arrangement of atoms in a crystal structure, as mentioned previously. This arrangement of atoms in crystals is called a lattice.
In 2-dimensions a plane lattice consists of an orderly array of points. The array is defined by the spacing between points and the directions (or angles) between the points. Thus, the array can be reproduced by specifying the distance and angle to move from point to point. This is referred to as translational symmetry. In the example here, the array is reproduced by moving down a distance a and moving to the right a distance b. The angle between the two directions of translation in this case is 90°





In the example to the right, the translation distances a and b are not equal and the translation angle is not 90°.

Crystals, of course, are made up of 3-dimensional arrays of atoms. Such 3-dimensional arrays are called space lattices. We discuss these space lattices in 3-dimensions in much more detail later. For now, however, we will continue to look a plane lattices and note that everything that applies to these 2-dimensional lattice also applies to space lattices.

There are four important points about crystal lattices that are noteworthy for our study of crystals:

1. Crystal faces develop along planes defined by the points in the lattice. In other words, all crystal faces must intersect atoms or molecules that make up the points. A face is more commonly developed in a crystal if it intersects a larger number of lattice points. This is known as the Bravais Law.


For example, in the plane lattice shown at the right, faces will be more common if they develop along the lattice planes labeled 1, somewhat common if they develop along those labeled 2, and less and less common if they develop along planes labeled 3, 4, and 5.





2. The angle between crystal faces is controlled by the spacing between lattice points.

As you can see from the imaginary 2-dimensional crystal lattice shown here, the angle q between the face that runs diagonally across the lattice and the horizontal face will depend on the spacing between the lattice points. Note that angles between faces are measured as the angle between the normals (lines perpendicular) to the faces. This applies in 3-dimesions as well.





Changing the lattice spacing changes the angular relationship. The lattice shown here has the same horizontal spacing between lattice points, but a smaller vertical spacing. Note how the angle f between the diagonal face and the horizontal face in this example is smaller than in the previous example.




3. Since all crystals of the same substance will have the same spacing between lattice points (they have the same crystal structure), the angles between corresponding faces of the same mineral will be the same. This is known as the Law of constancy of interfacial angles, as discussed previously.

4. The symmetry of the lattice will determine the angular relationships between crystal faces. Thus, in imperfect crystals or distorted crystals where the lengths of the edges or faces of symmetry related faces are not equal, the symmetry can still be determined by the angles between the faces.

In the example shown here, the upper diagram shows a perfect crystal with the symmetrically related faces have equal lengths. The low diagram shows a crystal built on the same lattice, but with distorted faces. Note that the angles between faces in the distorted crystal are the same as in the perfect crystal.




In order to know which faces on different crystals are the corresponding faces, we need some kind of standard coordinate system onto which we can orient the crystals and thus be able to refer to different directions and different planes within the crystals. Such a coordinate system is based on the concept of the crystallographic axes.



Crystallographic Axes

The crystallographic axes are imaginary lines that we can draw within the crystal lattice. These will define a coordinate system within the crystal. For 3-dimensional space lattices we need 3 or in some cases 4 crystallographic axes that define directions within the crystal lattices. Depending on the symmetry of the lattice, the directions may or may not be perpendicular to one another, and the divisions along the coordinate axes may or may not be equal along the axes. As we will see later, the lengths of the axes are in some way proportional to the lattice spacing along an axis and this is defined by the smallest group of points necessary to allow for translational symmetry to reproduce the lattice.

We here discuss the basic concepts of the crystallographic axes. As we will see, the axes are defined based on the symmetry of the lattice and the crystal. Each crystal system has different conventions that define the orientation of the axes, and the relative lengths of the axes.

Unit Cells

The "lengths" of the various crystallographic axes are defined on the basis of the unit cell. When arrays of atoms or molecules are laid out in a space lattice we define a group of such atoms as the unit cell. This unit cell contains all the necessary points on the lattice that can be translated to repeat itself in an infinite array. In other words, the unit cell defines the basic building blocks of the crystal, and the entire crystal is made up of repeatedly translated unit cells.
In defining a unit cell for a crystal the choice is somewhat arbitrary. But, the best choice is one where:

1. The edges of the unit cell should coincide with the symmetry of the lattice.
2. The edges of the unit cell should be related by the symmetry of the lattice.
3. The smallest possible cell that contains all elements should be chosen.

For example, in the 2-dimensional lattice shown here there are 6 possible choices to define the unit cell, labeled a through f. The lattice has 2-fold rotational symmetry about an axis perpendicular to the page. Since the lattice itself does not have 3-fold or 6-fold rotational symmetry, choices a and b would not be wise choices for the unit cell. Choice f can be eliminated because it is really just half of cell b. The edges of c and e are not coincident or parallel to any 2-fold axes that lie in the plane of the page. Thus our best choice would cell d.



Once we have chosen a unit cell for the crystal, then it can be oriented on the crystallographic axes to define the angles between the axes and to define the axial lengths. This will allow us to define directions within the crystal that become important when we realize that many properties of crystals depend on direction in the crystal. Properties that depend on direction in the crystal are called vectorial properties. We'll discuss these in a later lecture.

Another important point is that the relative lengths of the crystallographic axes, or unit cell edges, can be determined from measurements of the angles between crystal faces. We will consider measurements of axial lengths, and develop a system to define directions and label crystal faces in the next lecture.

http://www.tulane.edu/~sanelson/eens211/crystalmorphology&symmetry.htm

Edymar Gonzalez A

19.502.773

CRF

Translational symmetry breaking and valence-bond-solid (VBS) order in doped antiferromagnets

The theoretical strategy of these works is summarized in Figure 1.

Figure 1. Experimentally, the high temperature superconductors are produced by doping the insulating compound La2CuO4 with mobile holes. However, in this process, one crosses a quantum phase transition at which long-range magnetic order disappears. Theoretically it is more convenient to first destroy the magnetic long-range order in the insulator by some other mechanism (e.g. by adding frustrating magnetic interactions), and to then dope with mobile carriers: this two-step theoretical process is sketched above. Details of the first step are discussed elsewhere in these web pages, while the second step is described in the papers below.

The first theoretical step in Figure 1 was discussed elsewhere in these web pages: it was predicted in early work that destroying Neel order in insulating, square lattice antiferromagnets leads to the appearance of spin-Peierls order (or more generally valence-bond-solid (VBS) order). In addition, such paramagnetic insulators also necessarily possess a sharp S=1 collective spin resonance, and the confinement of a S=1/2 moment near each non-magnetic impurity (discussed elsewhere). The papers below discuss the consequences of doping such a VBS state by mobile holes: VBS order, confinement of S=1/2 moments near non-magnetic impurities, and the sharp S=1 resonance survive for a finite range of doping, and co-exist with d-wave-like superconductivity.

A first analysis of the doping of the non-magnetic VBS-ordered Mott insulator appeared in paper 2, and the results are summarized in Figure 2 below.

Figure 2. Phase diagram from paper 2 of the doping of a VBS-ordered Mott insulator, as described by the t-J model. It is instructive to follow the phases as a function of the doping d for large values of t/J. Initially, there is a superconducting state which coexists with VBS ordering. Here the superconducting order is d-wave like (that is, the pairing amplitudes in the x and y directions have opposite signs) and it coexists with VBS order: such a state was first discussed in paper 2. With increasing doping, the amplitude of the VBS order decreases and gapless fermionic excitations appear at nodal points, which are first generated at the edges of the Brillouin zone. Eventually there is a phase transition to an isotropic d-wave superconductor. The computation also found an instability to phase separation below the dotted line.

A more complete analysis of the phase diagram requires a more careful consideration of the influence of the long-range Coulomb interactions, and of the possibility of VBS-ordered states with larger periods. Such an analysis was carried out in papers 3,4, and the results are summarized in Figure 3 below.

Figure 3. Phase diagram analogous to Figure 1 above from papers 3,4. The vertical axis represents an arbitrary short-range exchange interaction which can destroy the long-range Neel order in the insulator. A specific example is the study of A. W. Sandvik, S. Daul, R. R. P. Singh, and D. J. Scalapino, Physical Review Letters 89, 247201 (2002), which used a ring exchange interaction: as expected from the arguments in this web page, the large ring exchange phase had VBS order, as shown in the figure above. The computations of papers 3,4 were carried out in the unhatched region (which has no long range magnetic order) and sample configurations of the VBS order are shown; the states shown pick one directions as special, but "checkerboard" states also appear (M. Vojta, Physical Review B 66, 104505 (2002)). The physics of the transition from the hatched to the unhatched regions (involving restoration of spin rotation invariance) is discussed in the web pages on collinear magnetic order, non-collinear magnetic order, quantum criticality, and the influence of an applied magnetic field . While the mean-field studies of VBS order lead to a bond-centered modulation of the lattice spacings (shown above), there can be "resonance" between different mean-field configurations, and the symmetry of bond modulations can also be such that the reflection symmetry is about a site.

Notice the more elaborate types of VBS order in the non-magnetic superconductor. It is expected that the primary modulation in these VBS-ordered states will be in the exchange, kinetic, and pairing energies between sites, rather than the on-site charge densities. This issue should be distinguished from the issue of the lattice symmetry of the modulation, which could have a plane of reflection symmetry about either the bonds or the sites.

While the VBS states discussed above break the symmetry between the x and y lattice directions, they are not necessarily ``quasi one-dimensional'' i.e. the basic instability leading to VBS ordering in the undoped paramagnet is genuinely two-dimensional. Furthermore, "checkerboard" states can also appear (M. Vojta, Physical Review B 66, 104505 (2002)).

http://qpt.physics.harvard.edu/vbs.html

Edymar Gonzalez A

19.502.773

CRF

What angle-resolved photoemission experiments tell about the microscopic theory for high-temperature superconductors

Author Affiliations

Contributed by Elihu Abrahams


Abstract

Recent angular-resolved photoemission experiments on high-temperature superconductors are consistent with a phenomenological description of the normal state of these materials as marginal Fermi liquids. The experiments also provide constraints on microscopic theories.

The discovery of the copper oxide superconducting materials in 1987 and the intense investigations that followed have raised some fundamental questions in condensed matter physics. These superconductors are characterized by two unexpected features. One is, of course, their unprecedented high transition temperatures (T c). In addition, it is clear that their normal-state properties are not those of ordinary metals; they are not consistent with the traditional Fermi-liquid quasiparticle picture that is a cornerstone of our understanding of the metallic state.

Many theoretical ideas have been proposed in response to these observations, but it has been difficult, on the basis of the experimental evidence, to identify the correct picture. However, recent angle-resolved photoemission (ARPES) experiments show a remarkable consistency with predictions (1, 2), made in 1989, based on a phenomenological characterization of these materials as “marginal Fermi liquids” (MFL). The aim of this communication is to discuss some aspects of these experiments and to point out what constraints they impose on possible microscopic theories.

The initial motivation for the MFL phenomenology was to understand simultaneously two quite different normal-state properties of these quasi-two-dimensional materials: the Raman scattering intensity, which measures the long wavelength response over a wide range of frequencies, and the nuclear magnetic relaxation rate of planar copper nuclei, which comes from magnetic fluctuations of low frequency and short wavelength. The underlying MFL assumption was that, at compositions for which the T c is highest (“optimal doping”), a sector of both the charge and magnetic excitation spectra χ(q,ω,T) has unusual properties: (i) The sector is momentum q independent over most of the Brillouin zone, and (ii) it has a scale-invariant form, as a function of frequency ω and temperature T, so that Imχ ∝ [f](ω/T) as follows:



N 0 is the density of energy states per unit volume, and ωc is a high-frequency cutoff. A central conclusion (1) is that the single-particle self energy caused by scattering from the excitation spectrum of Eq. 1 has a singular dependence on frequency and temperature but has unimportant momentum dependence. This self energy is calculated to be






where x ≈ max(|ω|,T) (for example, x = ), and λ is a coupling constant. The spectra of Eq. 1 could actually have a smooth dependence on q over a substantial part of the Brillouin zone. In that case, λ acquires a weak dependence on k. In the experiments discussed below, λ is in fact constant, within the experimental error. The most important point is that Σ2 remains proportional to x all around the Fermi surface.


In a Fermi liquid, quasiparticles are well defined, because the single-particle excitation decay rate (Σ2) is small compared with Σ1. Because in the present case Σ2, the imaginary part of the self energy, is only logarithmically smaller than Σ1, the real part, at T = 0, the appellation MFL was given (1). Here, the singular behavior of Σ leads to the result that there are no Fermi liquid-like quasiparticles; at T = 0, their “residue” z = [1 − ∂Σ1/∂ω]−1 vanishes at the Fermi surface (k = k F).

The earliest experimental data revealed that the transport properties in the normal state of the high-T c superconductors are unlike those of normal Fermi liquids, which have nonzero z. P. W. Anderson suggested (3, 4) that this experimentally observed anomalous normal-state behavior implies a non-Fermi liquid with z = 0. He developed this idea based on the separation of charge and spin energy scales and excitations. The MFL analysis is different and begins with a key assumption, Eq. 1, about the particle-hole excitation spectrum in both charge and magnetic (including spin) channels. Eq. 2 for the self energy follows from Eq. 1 with the following consequences:

•  A Fermi surface is defined at T = 0 as the locus of k points, where z→0 as (log ω)−1.

•  The single-particle scattering rate Σ2 is proportional to x≈max(|ω|,T).

•  The leading order contribution to Σ2 is independent of momentum both perpendicular to and around the Fermi surface. As discussed above, a weak smooth momentum dependence does not alter our conclusions.

In general, transport (e.g., electrical or thermal conduction) scattering rates have a different frequency and temperature dependence from that of the single-particle scattering rate Σ2, because the former emphasize backward scattering (large momentum transfer). However, the combination of momentum independence of Σ and the linear dependence on x of Σ2 in the MFL form of the self energy, Eq. 2, leads to a resistivity that is linear in T, as is seen in experiments on optimally doped materials. Other consequences of the MFL phenomenology include a temperature-independent contribution (with logarithmic corrections) to the thermal conductivity; an optical conductivity that falls off as with frequency as ω−1 (with logarithmic corrections), more slowly than the ω−2 dependence of the familiar Drude form; a Raman scattering intensity ∝ max(ω,T)/T; a T-independent contribution to the copper nuclear spin relaxation rate; and (in some geometries) a linear in bias voltage contribution to the single-particle tunneling rate. The MFL phenomenology has often been used to fit experiments, and it is found that the behavior of response functions is generally consistent with MFL as expressed in Eq. 1.

Nevertheless, although there were some direct indications of the correctness of Eq. 2 in early ARPES measurements (5), the MFL behavior of the single-particle excitation spectrum [i.e., Eq. 2] was not adequately confirmed. ARPES experiments measure the single-particle properties directly, in contrast to response functions, which are governed by joint two-particle (that is, particle-hole) properties. The quantity determined in ARPES experiments is the single-particle spectral function ��(k,ω), which depends on the self energy as follows:




The MFL behavior of the single-particle excitations has now been verified convincingly in the new ARPES experiments of Valla et al. (6) at Brookhaven National Laboratory and by Kaminski et al. (7) at Argonne National Laboratory. In the past, such measurements have been limited by energy and momentum resolution and large experimental backgrounds in the energy distribution measurements at fixed momentum (EDCs). These problems are now being overcome as new detectors have come on line. In particular, Valla et al. (6) have taken advantage of improved resolution to measure, on optimally doped Bi2Sr2CaCu2O8+δ, in addition to EDCs, momentum distributions at fixed energy (MDCs). In this way, the frequency dependence of the single-particle spectral function ��(k,ω) is measured at fixed k (EDC) and also the k dependence at fixed ω (MDC).

It follows from Eq. 3 that, if the self energy Σ is momentum independent perpendicular to the Fermi surface, then an MDC scanned along k perp for ω≈0 should have a lorentzian shape plotted against (k − k F)perp with a width proportional to Σ2(ω), and the Σ2 found in this way from MDCs should agree with that found by fitting EDCs. Furthermore, for an MFL, the width should be proportional to x = max(|ω|,T), where ω is measured from the chemical potential. This behavior has now been verified by Valla et al. (6). The fits of the MDCs at ω = 0 to a lorentzian are shown in Fig. 1 A. Fig. 1 B shows the linear variation of the width of the lorentzian with temperature.

Figure 1

(A) Momentum distribution curves for different temperatures. The solid lines are lorentzian fits. (B) Momentum widths of MDCs for three samples (circles, squares, and diamonds). The thin lines are T-linear fits. The resistivity (solid black line) is also shown. The double-headed arrow shows the momentum resolution of the experiment. Figure courtesy of P. D. Johnson (Brookhaven National Laboratory). Reproduced with permission from ref. 6 (Copyright 1999, American Association for the Advancement of Science)].

Preliminary data from both the Brookhaven (8) and Argonne (A. Kaminski, personal communication) groups also show that the contribution to Σ2, which is proportional to x as determined by scans perpendicular to the Fermi surface, is very weakly dependent on k̂ F; i.e., it varies only weakly with the angle on the Fermi surface. It is important to notice that there is no evidence of a T 2 contribution to Σ2 in the neighborhood of the Fermi surface anywhere in the Brillouin zone; the temperature-dependent part is always T linear.

Phenomenological ideas that seek to explain the transport anomalies in the cuprates on the basis of hot and cold spots on the Fermi surface are not consistent with this experimental finding, because they are based on having a T 2 behavior in the (1,1) direction and a T behavior in the (1,0) direction.

The Argonne group has plotted the EDCs together with fits to the MFL spectral function of Eq. 3 at over a dozen k-points between the (1,1) and (1,0) directions in the Brillouin zone. ImΣ(ω) is taken to be of the form Γ(k̂) + λ(k̂ F)ω. Γ represents an impurity contribution (see below). We show two typical examples in Fig. 2 A and B. These display, respectively, the results at the Fermi surface in the (1,0) and the (1,1) directions in the Brillouin zone that give the widest k̂ variations of Γ and λ. These self-energy parameters for the fit are given in the legend to Fig. 2.

Figure 2

Fits of the MFL self energy Γ+λℏω to the experimental data. Energies are in meV, with estimated uncertainties of ±15% in Γ and ±25% in λ. (A) The (1,0) direction, Γ = 0.12, λ = 0.27, and (B) the (1,1) direction, Γ = 0.035, λ = 0.35. Figure courtesy of A. Kaminski (Argonne National Laboratory). [Figure courtesy of A. Kaminski (Argonne National Laboratory), used by permission.]

Thus, the results for MDCs as well as EDCs may be summarized by the following expression: Formula The first term on the right-hand side of Eq. 3 is independent of frequency and temperature and is properly considered as the scattering rate because of static impurities. This can depend on k̂ F, the direction of k around the Fermi surface, as explained below. The second term is the MFL self energy of Eq. 2, a function only of x = max(|ω|,T); however a weak dependence on k̂ is possible, as discussed earlier. There may be additive analytic contributions of the normal Fermi-liquid type as well.

The dependence of the impurity scattering on k̂ F can be understood by the assumption that in well-prepared cuprates, the impurities lie between the CuO2 planes and therefore give rise to small-angle scattering (small momentum transfer) only. If the distance of the impurities to the CuO2 plane is D, then the characteristic scattering angle is δθ≈(2k F D)−1 [≈O(a/d)], where a and d are the in-plane and c-axis lattice constants). The single-particle impurity scattering rate Γk at a point k is then proportional to δθ about that point. For small δ θ, this gives the scattering rate Γk proportional to the local density of states at that k. It is known from both band structure calculations and ARPES experiments that the local density of states is about an order of magnitude larger in the (π,0) direction than in the (π,π) direction. Therefore, we expect the impurity contribution to increase as one turns k̂ around the Brillouin zone toward the (π,0) region. This is seen in preliminary data from the Brookhaven group as well as the Argonne group, which also show that the MFL contribution proportional to x has only weak dependence on k̂ F, if any (ref. 8; A. Kaminski, personal communication).

This assumption about the nature of impurity scattering also explains the well-known fact that the impurity contribution to the resistivity of well-prepared optimally doped cuprates is anomalously small. An impurity contribution to the single-particle scattering rate does not necessarily appear in the transport scattering rate, because the latter depends only on large momentum transfers. Thus the transport rate, emphasizing as it does the large-angle scattering, is proportional to δθ3, thus a factor δθ2 (perhaps as small as 0.04) smaller than Γ. In fact, it is known that impurities like Zn, which replace Cu in the plane, give a large contribution to the resistivity (9).

Some properties at optimum doping, for example the temperature dependence of the Hall resistivity, do not follow from the MFL self energy, Eqs. 2 and 4. Although the ARPES experiments indicate that the MFL form of the self energy is necessary, it is not sufficient to characterize all of the normal state properties at optimum doping.

The negligible (or weak) experimentally observed momentum dependence of the singular part of the single-particle self energy constrains theories of the normal state of the cuprate superconductors. We have discussed how the MFL phenomenology is consistent with the experiment. There are at least three classes of theories in which (in contrast to MFL) the self energy has strong momentum dependence: (i) Theories that involve strongly momentum-dependent couplings such as antiferromagnetic spin fluctuation exchange (10). (ii) Theories based on breaking of translational symmetry, such as stripe or charge-density wave scenarios (11, 12). (iii) Theories based on an extension from one to two dimensions of anomalous non-Fermi liquid behavior as described in the Luttinger liquid formulation (13). In the first case, coupling involving an excitation whose spectrum is peaked in one part of the Brillouin zone necessarily leads to a momentum-dependent self energy. In the second case, the breaking of translation invariance also results in momentum dependence of all quantities. The third case, the Luttinger liquid, has nonanalytic dependence of the spectral function on momentum, that is on k − k F, at ω = 0 that is the same as the ω dependence at k = k F (14). Thus, should the new ARPES results prove robust, these three classes of theories would require important modifications.

In the theory of the MFL, the max(|ω|,T) dependence of both the single-particle and transport rates comes about from a particle-hole fluctuation spectrum that both is scale invariant in frequency and has negligible momentum dependence as in Eq. 1. A direct experimental verification of the basis for MFL, that is, of a scale-invariant fluctuation spectrum as in Eq. 1 is as yet incomplete. Although such a spectrum is observed at long wavelengths in Raman scattering, it has not yet been clearly identified at larger momentum. Experimental methods to measure the charge fluctuation spectrum at large momentum are not well developed. The magnetic part of the spectrum (because of both orbital and spin fluctuations) is in principle observable in neutron scattering. However, the signal-to-noise and background problems for a featureless inelastic spectrum spread over ωc≈0.5 eV are formidable. At the same time, the fact that a magnetic fluctuation spectrum of the MFL form accounts for the longitudinal NMR relaxation rate of planar copper nuclei near optimum doping does give support to Eq. 1 for large momenta.

It is not clear to us how the observed ARPES spectra (and the fact that the transport scattering rate has the same temperature and frequency dependence as the single particle scattering rate) can come about except in a theory that results in the scale-invariant form essentially as specified by Eq. 1. It is suggestive that a scale-invariant fluctuation spectrum generally arises in a region about a quantum critical point (QCP). The momentum independence of Eq. 1 specifies that if a QCP underlies the MFL behavior, then the associated dynamical critical exponent zd → ∞. As stressed elsewhere (15, 16), the experimental phase diagram in the temperature-doping plane is consistent with the existence of a QCP at a doping near that of the highest critical temperature. A microscopic theory for a QCP with properties similar to the MFL spectrum of Eq. 1 has been presented and shown also to promote d-wave superconductivity (15, 16). Some unique predictions of that theory await experimental tests.

http://www.pnas.org/content/97/11/5714.full

Edymar Gonzalez A

19.502.773

CRF