estructura cristalina

Estructura Cristalina

Un sólido cristalino, o cristal, es una ordenación periódica de estructuras idénticas. La estructura idéntica que se repite, recibe el nombre de base cristalina. La estructura sobre la que se repite, el de red cristalina, (Fig.1.1).

Tres vectores, a, b y c definen una red cristalina a través de tres enteros n₁, n₂y n₃, de modo que si es el vector de posición de un punto de la red, el expresado por:

(1.1)

también lo es. El vector

(1.2)

define el grupo de traslaciones del cristal.

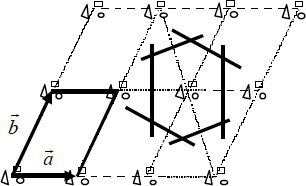
Figura 1.1.- Cristal, celdilla primitiva y celdilla de Wigner- Seitz en dos dimensiones

En toda red cristalina se pueden encontrar (y no de forma única) tres vectores de forma que dos puntos reticulares cualesquiera están siempre relacionados por una expresión del tipo (1.1) con n₁, n₂y n₃ enteros. Los vectores a, b y c que cumplen también esto, definen una celdilla que también por traslación genera el cristal. Se la llama celdilla primitiva porque es la de volumen mínimo que por traslación reproduce el cristal. Si hubiera otra de menor volumen y tomando n₁, n₂y n₃ enteros, no encontraríamos necesariamente un punto reticular (Fig. 1.1). Es fácil comprender que a cada celdilla primitiva le corresponde un solo punto reticular (con su correspondiente base cristalina).

La celdilla primitiva no es única. Una forma de concretar la celdilla primitiva es bisecar por planos los segmentos que unen un punto reticular a sus próximos vecinos. En este caso recibe el nombre de celdilla elemental de Wigner-Seitz (Fig. 1.1) y cumple con los postulados anteriores. En particular, es evidente que sólo contiene un punto reticular.

Las redes cristalinas se llaman también redes de Bravais y hay 14 diferentes agrupadas en 7 sistemas cris talinos (Fig. 1.2).

Sistema	Redes	Malla	Redes de Bravais
Cúbico	Simple Centrado en cuerpo Centrado en caras	a = b = c α = β = γ = 90º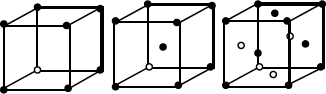
Trigonal	Romboédrico	a = b = c α = β = γ ≠ 90º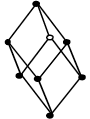
Hexagonal	Simple	a = b ≠ c α = β = 90º γ ≠ 120º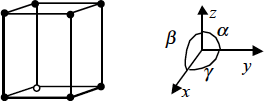
Tetragonal	Simple Centrado en cuerpo	a = b ≠ c α = β = γ = 90º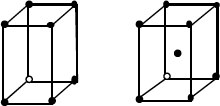
Ortorrómbico	Simple Centrado en bases Centrado en cuerpo Centrado en caras	a ≠ b ≠ c α = β = γ = 90º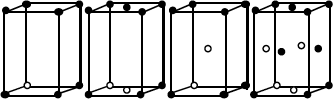
Monoclínico	Simple Centrado en bases	a ≠ b ≠ c α = β = 90º ≠ γ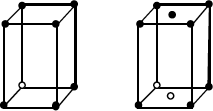
Triclínico	Simple	a ≠ b ≠ c α ≠ β ≠ γ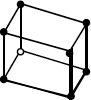

Figura 1.2.- Propiedades de las redes de Bravais

De ellos el sistema cúbico es el de máxima simetría y además el sistema de los semiconductores usuales. Más concretamente estos cristalizan en el sistema cúbico centrado en caras (fcc) que puede verse en la Figura 1.2. Tienen asociada, normalmente, una base cristalina de dos átomos que pueden ser iguales (como en los semiconductores elementales: Silicio, Germanio…) o diferentes (Arseniuro de Galio, Fosfuro de Indio y otros semiconductores formados por asociación de elementos de los grupos III y V, o II y VI del sistema periódico). Para este caso se representa en la Fig. 1.3 la estructura atómica de un material diatómico (tipo blenda, que es la estructura cúbica del SZn). Es fácil ver que los átomos "blancos" marcan la estructura fcc y que cada átomo blanco tiene asociado otro "negro". Cuando todos los átomos son iguales tenemos el caso de las estructuras del tipo diamante.

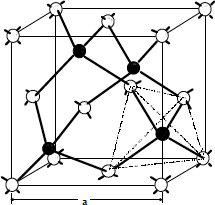
Figura 1.3.- Estructura diatómica fcc

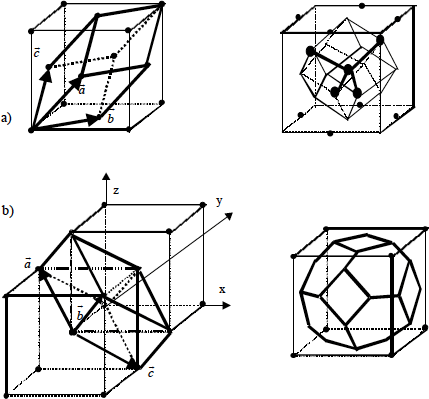
Figura 1.4.- Vectores primitivos de la red fcc (a) y bcc (b).
Respectivas celdillas de Wigner-Seitz.

Puede verse que esta estructura es compatible con enlaces de tipo tetraédrico, típico de los enlaces covalentes entre orbitales sp³. Una celdilla primitiva puede ser un romboedro, mientras que la celdilla de Wigner-Seitz es un dodecaedro rómbico regular (Fig.1.4). En la Tabla 1.1 se dan los parámetros de red (lado del cubo del sistema) para algunos semiconductores usuales.

TABLA 1.1.- Parámetros de red de semiconductores fcc

Semiconductor	a (Å)	Semiconductor	a (Å)
Diamante	3.6680	GaP	5.4504
SiC - (3C)	4.3596	GaAs	5.6533
Si	5.4307	InAs	6.0584
Ge	5.6575	InP	5.8688

Algunos semiconductores de interés actual cristalizan en el sistema hexagonal. Son semiconductores que presentan enlaces de tipo tetraédrico, semejantes a los del Silicio. En la Figura 1.5a se representa este tipo de estructura, que se conoce con el nombre de Wurtzita (que es la forma hexagonal del sulfuro de zinc, SZn.). La estructura puede obtenerse a partir de prismas de base rómbica, de 60º de ángulo.

Normalmente se le asocian cuatro ejes: a₁ , a₂ y a₃ , que forman entre sí ángulos de 120º y un cuarto eje, c , normal a los anteriores. Puede observarse, también, que la red hexagonal procede del empaquetamiento compacto. La formación de este tipo de estructura puede imaginarse a partir de la colocación de diferentes capas de bolas en una caja: cada bola de una capa es tangente a seis de la misma capa, se apoya en tres de la capa inferior y, con otras dos de su capa, soporta una bola de la superior. Según la posición relativa de las diferentes capas (secuencia de deposición) pueden obtenerse diferentes redes hexagonales y una cúbica centrada en caras, coincidiendo el eje cr con la dirección (1,1,1). Con la periodicidad según cr , reciben diversos nombres: 2H, 3C, 4H, 6H ... .

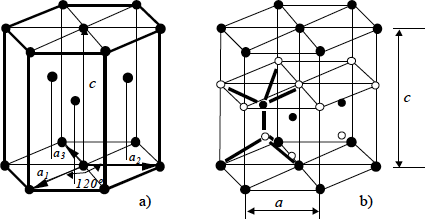
Figura 1.5.- Red hexagonal : a) Estructura cristalina y b) estructura atómica (enlaces tetraédricos)

• LA RED RECÍPROCA

Para cada cristal su red de Bravais constituye la red directa. Asociada a ella existe la red recíproca.

Dados tres vectores (primitivos) de la red directa se obtienen los tres vectores base de la red recíproca por las relaciones:

(1.3)

que verifican

(1.4)

donde δ_ij es la delta de Krönecker, que toma el valor 1 cuando los dos subíndices son iguales y 0 en todos los demás.

Como ejemplo puede comprobarse que la red recíproca de una cúbica centrada en caras, es otra centrada en el cuerpo y viceversa (Fig. 1.4). También la red recíproca admite varias celdillas primitivas. Entre ellas es posible construir la de Wigner-Seitz, que en este caso recibe el nombre de 1ª Zona de Brillouin.

• PROPIEDADES DE LA RED RECÍPROCA: ÍNDICES DE MILLER

Sea T* r un vector de traslación de la red recíproca, que expresamos en la forma

con m1, m2 y m3 enteros.

Sea T_N un vector de traslación de la red directa que expresamos en la forma (1.2)

Entonces:

• Familias de planos y direcciones.

El producto

, de acuerdo con (1.4), vale

siendo N, evidentemente, un número entero.

Para cada valor del producto , y dado un vector T* , existen infinitos vectores , cuya proyección sobre es la misma, que cumplen que y cuyas componentes son raíces de la ecuación diofántica:

En la Fig. 1.6 se representa una interpretación geométrica (bidimensional) de este hecho en la que se ha tomado el origen en un punto reticular. Con esta condición los vectores definen puntos reticulares contenidos en un plano que es normal a .

, para todos los valores enteros de N, define una dirección en el cristal [m₁, m₂, m₃] y una familia de planos reticulares normales a ella (m₁, m₂, m₃).

• Distancias entre planos de la familia

Si m₁, m₂, m₃ no tienen factores comunes, dos valores consecutivos de N (N y N+1) definen dos planos consecutivos de la familia y la distancia, d, entre ellos será tal que

es decir:

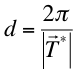(1.5)

siendo y vectores de los puntos reticulares de los planos correspondientes a N y N+1.,

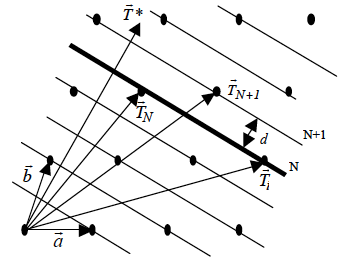
Figura 1.6.- Planos reticulares e índices de Miller

• Casos particulares: Índices de Miller

Es interesante ver cual es la intersección de la familia de planos sobre los ejes. Si la familia interseca a los ejes ar,br y cr con intervalos d₁, d₂ y d₃ (Fig. 1.5), medidos cuando se toma como unidad , , , respectivamente, se tendrá que:

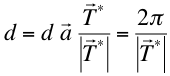
o sea:

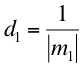
ya que ; y así también para b y c.

Es decir, la familia de planos interseca a los ejes a distancias proporcionales a 1/m₁, 1/m₂ y 1/m₃ (en términos del espaciado de la red).

Dicho de otra forma m₁, m₂ y m₃ son proporcionales a los inversos de las mencionadas distancias.

Si además se escogen los menores posibles (es decir, sin factores comunes), verifican (1.5) y, desde luego, definen una dirección y una familia de planos.

Además, se llaman índices de Miller, que se suelen denotar ordinariamente por (h,k,l). Este símb olo también indica la familia de planos, mientras que [h,k,l] precisa una dirección en el cristal.

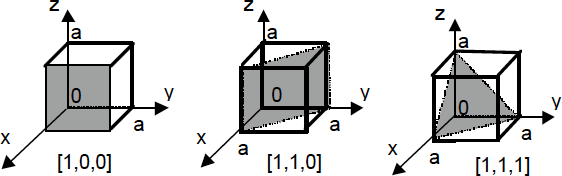
Figura 1.7.- Índices de Miller en una red cúbica.

Un signo - sobre un índice indica que la intersección se ha verificado en el sentido negativo del eje.

Se usan también los símbolos:

{h,k,l} para indicar los planos de simetría equivalentes y

para indicar las direcciones equivalentes.

Por ejemplo [0,1,0], [0,0,1], [1,0,0].

En la Fig. 1.7 se representan los índices de Miller más usados y que corresponden a una red cúbica simple.

Para la red hexagonal de la Figura 1.5 y por excepción, al emplear cuatro ejes, los índices de Miller no son tres, sino cuatro. El eje c marca la dirección [0,0,0,1].

Defectos Estructurales de los Cristales

No existen, obviamente, cristales absolutamente perfectos. La periodicidad de la red se ve rota, aparte de por la finitud del cristal, por la presencia de defectos que se generan en el crecimiento del cristal y/o los procesos tecnológicos que sufre el material
hasta convertirse en un circuito integrado.

Por otro lado no es factible la realización del cristal de pureza 100%, ni es interesante para la Electrónica, como veremos. Brevemente, los defectos estructurales pueden clasificarse en:

• Defectos puntuales

Corresponden a desviaciones de la situación ideal que afectan a las bases cristalinas y/o los puntos reticulares.

Como defectos puntuales de naturaleza meramente estructural o cristalográfica están las lagunas o vacantes (también llamados defectos Schottky) y los defectos intersticiales, que se producen por la ausencia de un átomo de su punto reticular o por la presencia de un átomo en un lugar del cristal que no es un punto reticular, respectivamente.

La asociación de una laguna y un intersticial se conoce con el nombre de defecto de Frenkel (Fig. 1.8).

Las lagunas y los intersticiales son una consecuencia de la energía (de vibración) de la red, que aumenta con la temp eratura. La concentración de lagunas o intersticiales puede expresarse, en una forma simple, a través de una ley del tipo de Arrhenius, en la forma

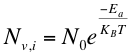
donde E_a es la energía de activación de la formación de la laguna o el intersticial. El factor pre-exponencial para los semiconductores simples puede ser considerado como la densidad atómica del material. En la Tabla 1.2 se dan algunos valores de estos parámetros. Es muy fácil calcular el insignificante número de este tipo de defectos a la temp eratura ambiente.

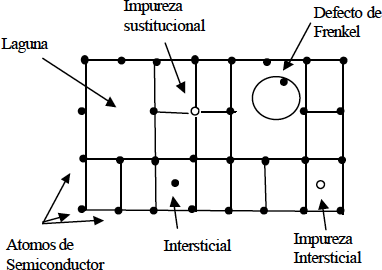
Figura 1.8.- Defectos puntuales

TABLA 1.2.- Parámetros de defectos puntuales

Tipo de defecto	Factor pre-exponencial, N0 (cm-3)	Energía de activación Ea (eV)
Laguna en Silicio	5.02 10 22	2.6
Intersticial en Silicio	5.02 10 22	4.5
Laguna de galio en AsGa	3.3 10 18	0.4
Laguna de arsénico en AsGa	2.2 10 20	0.7

A estos defectos hay que añadir, y para los semiconductores binarios, ternarios …, los llamados defectos de antisitio o antiestructurales que corresponden a situaciones en las que un sitio de un átomo está ocupado por otro de naturaleza distinta (por ejemplo, en lugar de un átomo de Galio, hay uno de Arsénico).

Finalmente y de naturaleza puntual es también el defecto creado por la presencia de impurezas que pueden ocupar un lugar sustitucional o intersticial. Y también formar complejos o asociaciones con otros defectos puntuales. Las impurezas, dada su naturaleza diferente de la del cristal, se conocen también como defectos extrínsecos, por contraposición a los otros o intrínsecos.

• Defectos bidimensionales

Son defectos asociados a la estructura y organización de los planos reticulares. Principalmente están constituidos por las dislocaciones, los defectos de apilamiento (stacking faults), los planos de simetría (twins) y los defectos de deslizamiento.

Las dislocaciones son defectos asociados a la presencia de planos reticulares anómalos en el cristal, tanto por su ubicación como por su orientación. En la Fig.1.9 se representan las dislocaciones de tornillo, de borde y de acoplo. En el primer caso se ha producido un desplazamiento progresivo de parte del cristal. En el segundo un nuevo plano cristalino se ha insertado a partir de una determinada posición. Las dislocaciones de acoplo se producen en heteroestructuras cuando se realiza la unión de dos materiales diferentes en los que, obviamente, los parámetros reticulares no coinciden.

Su principal fuente de formación es la tensión termomecánica del cristal durante el crecimiento. Pero también pueden producirse por acumulación de defectos puntuales. Cuando la temperatura es elevada, la energía del cristal puede desplazar los átomos del mismo en el entrono de la dislocación. Esto genera el movimiento de las mismas y/o la modificación de su tamaño y estructura.

Hoy es posible encontrar cristales "libres" de dislocaciones (<500>

También existen, asociados a planos reticulares, defectos de apilamiento (stacking faults). En la Fig. 1.10a se muestra un corte (1,1,0) de capas apiladas en la dirección <1,1,1> . Hay seis (tres dobles) capas atómicas de diferente configuración; luego, el cristal se repite. En una región localizada del cristal existe un error de apilamiento cuando desaparece un plano atómico de una doble cara junto con el adyacente de otra (por ejemplo los planos marcados con Aa, Bb o Cc), como se ve en la Figura 1.10b: Se genera una doble capa que es diferente de las otras del cristal. Nótese que una dislocación correspondería a la inclusión de una capa doble del tipo Ab.

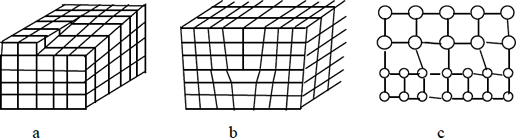
Figura 1.9.- Dislocaciones de tornillo (a), de borde (b) y de acoplo (c)

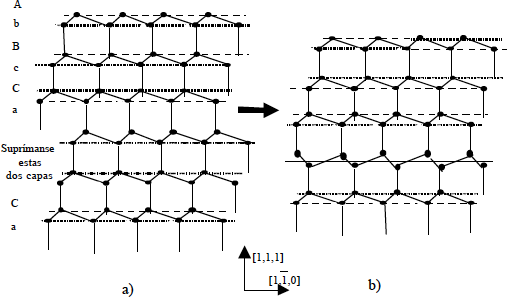
Figura 1.10.- Defectos de apilamiento intrínseco (Intrinsic stacking faults)

Este defecto de apilamiento se conoce como intrínseco (ISF). A veces, aparece un plano“extra” en un proceso inverso al anterior. Entonces el defecto y el plano se conocen como extrínsecos (ESF).

Los "twins" o planos de simetría (también, planos de composición) se generan por el cambio de orientación del cristal a partir de ellos. En la Fig. 1.11 se muestra esquemáticamente esta situación, que puede producirse por un simple desplazamiento de los átomos del cristal, en la que puede verse que parte del cristal resulta simétrico con relación al anterior.

Finalmente y por la semejanza en lo que estamos exponiendo debemos mencionar los defectos de deslizamiento, que se representan en la Fig. 1.12. En el caso ideal, una parte del cristal desliza sobre otra a lo largo del plano de deslizamiento y no aparecen otros defectos. Pero con bastante frecuencia no toda una parte desliza, sino solo una fracción de ella, lo que produce tensiones y finalmente dislocaciones y otros defectos.

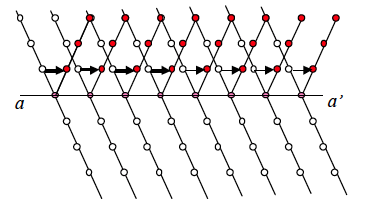
Figura 1.11.- Panos de simetría (twins)

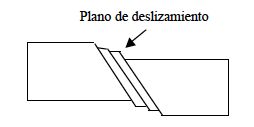
Figura 1.12.- Deslizamientos

A veces aparecen microdefectos que pueden considerarse como lazos de dislocaciones de tamaño muy pequeño (entre 500Å y 3mm). Aparecen generalmente en la superficie de la oblea. Su naturaleza no está muy clara, pero pudieran estar asociados a precipitados de asociaciones heterogéneas de átomos intersticiales de semiconductor y carbono u oxígeno. O también de otras impurezas.

• Defectos superficiales

Cuando los defectos se extienden a una superficie importante del cris tal, se llaman defectos superficiales. Principalmente son las fronteras de grano y las superficies laterales. Las primeras separan dos zonas del cris tal que no guardan relación en su orientación cristalográfica y que reciben el nombre de granos y son inclusiones de microcristales en el monocristal.

Las segundas son las superficies que limitan el cristal finito y que presentan, en el mejor de los casos, enlaces atómicos rotos y una ruptura de la periodicidad del cristal. En los capítulos que siguen tendremos ocasión de ver la importancia de los elementos de simetría de los cristales y, en particular, la de la periodicidad. Todos los defectos, de una forma o de otra, rompen esta periodicidad. Y, muy principalmente, las superficies laterales (un cristal perfectamente periódico debería ser infinito).

Los defectos cambian, en mayor o menor medida, las propiedades del cristal y su importancia en los aspectos electrónicos de los semiconductores es diferente. Los defectos asociados a las impurezas son necesarios e imprescindibles cuando pueden ser controlados, porque son defectos que generalmente demuestran una actividad eléctrica, capturando o emitiendo electrones. Es decir son capaces de aparecer como centros cargados en el cristal. Este comportamiento también está asociado a algunos defectos puntuales extrínsecos como las lagunas. En cambio otros defectos no exhiben actividad eléctrica. Pero todos, de una manera u otra interfieren en el proceso de la conducción eléctrica y en algunos casos en la tecnología de fabricación de dispositivos y circuitos, variando la cinética del proceso y disminuyendo su rendimiento. De ahí el interés de controlar la calidad del material.